Email titkosítás avagy az üzenet 🔒kódolása és 🔓 dekódolása
Az email titkosítás jelentőségére mutattam rá, 🔗„Melyik a legjobb email szolgáltató?” című írásomban.
ℹ️ Most viszont szeretnék segíteni a felhasználóknak abban, hogy megértsék a titkosítási folyamatok lényegi részét. Precíz információt leljenek ahhoz, hogy miként lehet beállítani eme titkosítási folyamatokat a különböző E-mail klienseken.
Az email klienseket egyenként természetesen nem fogom elemezni, ugyanis az alkalmazott elv a lényeg. Szinte mindegyik egy kaptafára megy.
Mi az Email titkosítás folyamatának elvi működése❓
✅ Akármelyik titkosítási szolgáltatást is nézzük:
- pGp (Pretty Good Privacy)
- pEp (Pretty Easy Privacy)
a lényeg a kulcspárban van, amit értelmezhetünk úgy, hogy kódolás / dekódolás.
- A kulcspár egyik részét PRIVÁT KULCSNAK (private key) hívjuk, s ez az amire nagyon vigyázni kell, soha ne adjuk ki senkinek,
- a másik részét pedig NYILVÁNOS KULCSNAK (Public Key) szokás nevezni, ami pont azért nyilvános, mert bárkinek odaadhatjuk.
Sőt, ezt a nyilvános kulcsot oda is kell adnunk, ha az illetővel szeretnénk titkosított levelezést folytatni❗
A pEp és pGp titkosítás rövid ismertetése
A pGp (Pretty Good Privacy) egy hibrid megközelítés. Amikor a felhasználói adatokat pGp-vel titkosítják, a pGp tömöríti a szöveget, ami nemcsak tárhelyt takarít meg, hanem növeli a biztonságot is.
Sok hackelési kísérlet próbálja olvasni a sima szöveget, de megbotlik a tömörített / kódolt információn.
A pGp létrehoz egy munkamenet-kulcsot, amely egyszeri felhasználású titkos kulcs. A szöveg titkosítva van, beleértve a munkamenet kulcsot is. A nyilvános titkosított munkamenetkulcsot a kódolt / titkosított szöveggel együtt elküldjük.
A vevő oldalán a visszafejtés fordított sorrendben működik. A címzett egy privát kulcsot használ a munkamenet-kulcs lekérésére, a pGp ezután dekódolja a titkosított kódot.
A pEp (Pretty Easy Privacy) titkosítási folyamataiba nem kívánok jobban belemélyedni, de jelzem
PgP kulcs generálás az email titkosítás érdekében
A privát és publikus kulcspár generálásához a Kleopátra alkalmazás használatát tanácsolom. Töltsük le egy megbízható forrásból a Gpg4win nevű programot:
🔗 https://www.gpg4win.org/get-gpg4win.html
Ez a programcsomag mindig tartalmazza a hivatkozott Kleopátra alkalmazás legfrissebb verzióját is. A program beállítható magyar nyelvre is, de a magyarítása 100% még nem ment végbe. Ezért is van az, hogy a Fájl menün belül számos almenüpont még angol nyelven maradt. A Kleopátra program Fájl menü New Keypair… almenüpontja lesz az amire szükségünk lesz a szóban forgó kulcspár létrehozásához.
Ha ezt alkalmazzuk akkor az alábbi dialógus ablakot kapjuk:
1. lépés
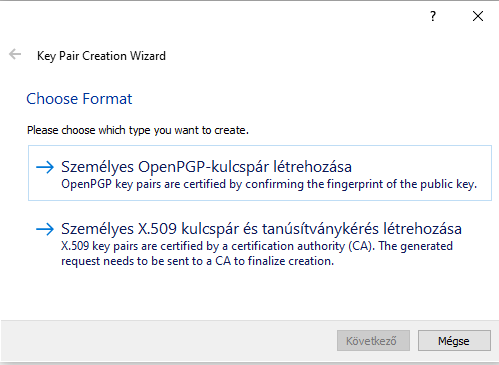
Tehát itt a kulcspár telepítés varázslónál válasszuk a „Személyes OpenPGP-kulcspár lérehozása” lehetőséget. Megadjuk a nevünket, email címünket.
Tanulmányozzuk a „Speciális beállítások” részt
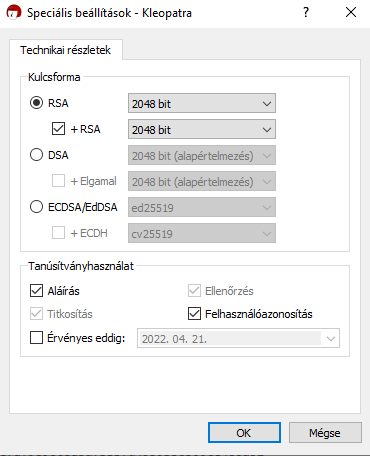✔️ Itt láthatjuk azokat a fontos technikai részleteket, amelyek alapján meghatározhatjuk, hogy milyen kódolási eljárást is alkalmazzunk pontosan.
RSA:
Az RSA egy nyílt kulcsú azaz aszimmetrikus titkosító algoritmus, amit még valamikor 1976-ban hozott létre Ron Rivest, Adi Shamir, és Len Adleman. Az RSA-titkosításhoz egy nyílt és egy titkos kulcs tartozik. A nyílt kulcs mindenki számára ismert, s ennek segítségével kódolhatják mások nekünk szánt üzeneteiket. A nyílt kulccsal kódolt üzenetet csak a titkos kulccsal tudjuk visszafejteni azaz dekódolni. Ha RSA kódolásról beszélünk – titkosítás, dekódolás, aláírás, stb. – akkor moduláris hatványozást végzünk.
Az RSA titkosítás alapjául szolgáló képlet
Egyszerűen leírva a képlet m = p * q ahol m lesz a modulusa mind a nyilvános mind a titkos kulcsnak egyaránt.
Az Euler függvényről
Az Euler függvény értéke tehát (p-1) * (q-1).
- Kiválaszt egy olyan e egész számot, amely relatív prím Φ(m)-hez (azaz a legnagyobb közös osztójuk 1).
- Kiszámít egy olyan d értéket, amelyre d * e = 1 (modulo Φ(m) teljesül, azaz, ha e és d szorzatát elosztjuk Φ(m)-mel, akkor 1-et kapunk maradékul. A nyilvános kulcs m és e a magánkulcs pedig d lesz.
✅ RSA esetén a kulcshosszt az m modulus méretével szokás megadni.
RSA 2048
Ha 2048 bites RSA-ról beszélünk, akkor m hossza 2048 bit, azaz p és q két 1024 bites prím. Célszerű, ha p és q hasonló nagyságrendbe tartozik. Ha az egyikük nagyon kicsi, akkor az RSA könnyebben támadható. Az e nyilvános kitevőt kicsinek szokás választani, míg d valószínűleg 2048 bites lesz.
Napjainkban az RSA 2048 vagy 4096 bites változata megfelelő védelmet tud nyújtani❗
Vajon mennyire esélyes a brute force?
Egy hagyományos számítógépnek ami bináris elven működik, tehát 0 vagy 1 értékekre rendezkedik be, másszóval van esemény vagy nincs esemény, egy életöltő is kevés lenne, hogy a „brute force” erejével feltörje a titkosítást.
A brute force azt jelenti, hogy hihetetlen kegyetlenül a számítógép, az összes lehetséges kombinációt szépen végig próbálgatja 😉
Egyes hacker csoportok nagyon kreatív módszereket alkalmaznak!
Különböző vírusos algoritmusokra épített trükkökkel próbálkoznak, hogy a gyanútlan emberek gépét megfertőzzék. Ezek a vírusok a háttérben gyakorlatilag zombigépet csinálnak a felhasználók gépéből,
amelyek rengeteg erőforrást fognak a CPU munkaszeletéből arra áldozni, hogy a háttérben végezzék a fentiekben ismertetett brute force műveletet.
Ahogy mondtam az RSA 2048 és 4096 nagyon jól véd
A hackerek ha a világ összes hagyományos számítógépét is egybekötnék, akkor is nagyon hosszú időbe,
például 10 évbe kerülne nekik a meló. 😊
A jelenlegi kriptográfiai eljárásokat maximum a távoli jövő – a Nasa vagy Google berkeiben már jelenleg is működő – 🔗Qubit számítógépek veszélyeztethetnék.
A kvantumbit esetén viszont olyan szuperpozíciókról beszélhetünk ahol nem csak a szokványos két állapot 1 – magas feszültség vagy 0 – alacsony feszültség vehető fel. A kvantumszámítógép alapegysége, a qubit (quantum bit) 0 és 1 között bármilyen értéket képviselhet, és nem csak egyetlen értéket, hanem egyidejűleg értékek sokaságát, szuperpozícióját!
📜 A Google 2019-ben elkészítette az 53 bites Qubit gépét, ami azt jelenti, hogy 2 53 eseményt tud egyszerre kezelni 😎 Szóval egy Qubit számítógép viszonylag egyszerűen tudná alkalmazni a brute force-t, és valószínűleg az emberöltőnyi időt redukálná pár órára.
De jelenleg azért még nem tartunk itt, s ahogy mondtam a fenti kriptográfiai megoldások tökéletesek.
Eme mese után, folytassuk a kulcspár előállítását, ami az email titkosítás lételeme
2. lépés
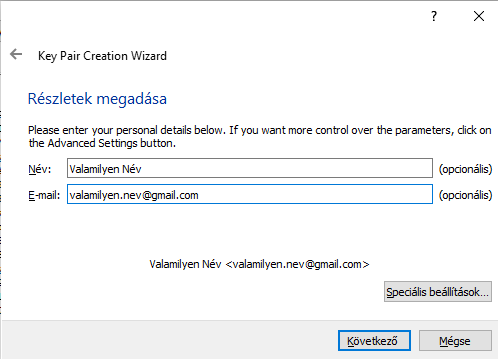
Ha a részletezett speciális beállításokban mindent beállítottunk úgy, ahogyan az nekünk jó, akkor klikkeljünk a
„Következő”
gombra. Fontos, hogyha azt szeretnénk, hogy a generált kulcspárunk érvényessége sose járjon le, akkor a speciális beállításoknál az „Érvényesség eddig:” előtti jelölőnégyzetből feltétlenül vegyük ki a pipát. Én azon a véleményen vagyok, ha a privát kulcsunkra nagyon jól vigyázunk és soha senkinek nem adjuk ki, akkor teljesen felesleges érvényességi időt beállítani.
A magyar nyelvi áttétel, lehet kicsit gyenge
Félreértés ne essék nem kívánom a magyar fordítást szapulni, hiszen szegénykék, teljesen ingyenesen önkéntes alapon járultak hozzá a magyarítás elkészítéséhez. Viszont megfigyelhető, hogy például a Név: és az E-mail: után (opcionális) megnevezés sem helytálló, hiszen eme két adat egyáltalán nem lehet opcionális.
A Részletek megadása alatt is látszik, hogy még maradtak benne angol nyelvű mondatok.
3. lépés
Az összesítések ellenőrzése
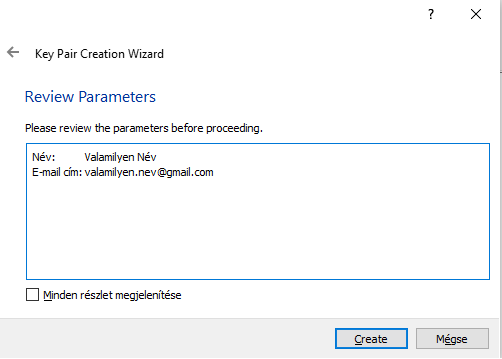Az összesítések ellenőrzéseMég ellenőrizhetjük a „Minden részlet megjelenítése” résznél az összesítést és eldönthetjük, hogy minden úgy fog-e végbe menni, ahogyan azt mi szeretnénk.
Jelmondat létrehozása
Nyomjunk rá a „Create” gombra aminek hatására az alábbi dialógus ablakot fogjuk kapni ⬇️
4. lépés
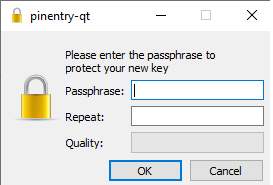
Itt meg kell adnunk egy jelmondatot (Passphrase) amit aztán a (Repeat) résznél pontosan úgy kell begépelnünk. Javaslom mindenkinek ezt a jelmondatot jegyezze meg, s a jelmondat tartalmazzon kis és nagybetűt, valamint számot is. Ezt érdemes egy cetlire felírni és bezárni a széfünkbe.
Ezt a jelmondatot az email kliens mindig kérni fogja tőlünk amikor egy levelet kódolva küldünk, vagy egy beérkezett kódolt levelet szeretnénk visszafejteni.
Sokak számára ez az 5 lépéses metodika ezért nem kényelmes, aminek az utolsó lépése itt van ⬇️
5. lépés
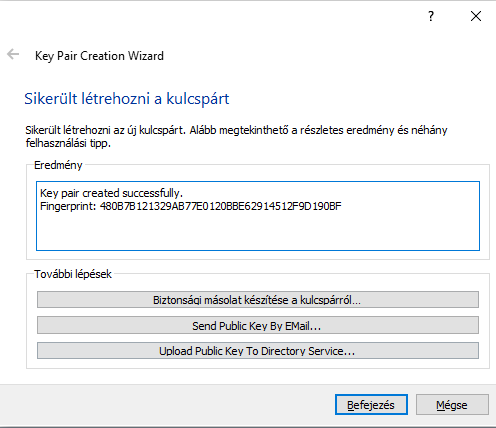
Biztonsági másolat a kulcspárról!
Javaslom, hogy készítsünk biztonsági másolatot a kulcspárról és azt a számítógépünk egy biztonságos helyére (könyvtár) mentsük le. Ez az eredmény egyébként egy .asc fájl lesz és ez egyben tartalmazza a privát és a nyilvános kulcsot egyaránt! Ezt az .asc fájlt az égvilágon ne osszuk meg senkivel, ezt kell importálnunk majd az email kliensünkkel (például a cikkben említett Thunderbird).
Szintén hasznos lépés ha élünk a „Send Public Key By EMail…” lehetőséggel, mert segítségével a nyilvános kulcsunkat (amit másnak is odaadhatunk) elküldhetjük magunknak email-re. Ugyanakkor a későbbiekben ismertetett Thunderbird email kliensnél ki fogok térni rá, hogyan tudjuk exportálni a nyilvános kulcsunkat!
Ha minden rendben is ment akkor „Befejezés” és ügye a kulcspárunk, amit a Biztonsági másolat készítése a kulcspárról gombra kattintva lementettünk számítógépünkre az szépen rendelkezésre is fog állni egy .asc fájl formájában.
Erre nagyon vigyázzunk mert ismétlem még egyszer ez tartalmazza a privát és nyilvános kulcsunkat egyben, tehát ezt senkinek nem szabad odaadni, kizárólag importálni fogjuk a Thunderbird Enigmail/p≡p kulcskezelőjével!
⬆️ A fentiekben vázolt 5 lépéses metodika helyett (a Kleopátra mellőzésével) létrehozhatunk akár JELMONDAT NÉLKÜLI kulcspárt is! ⬇️
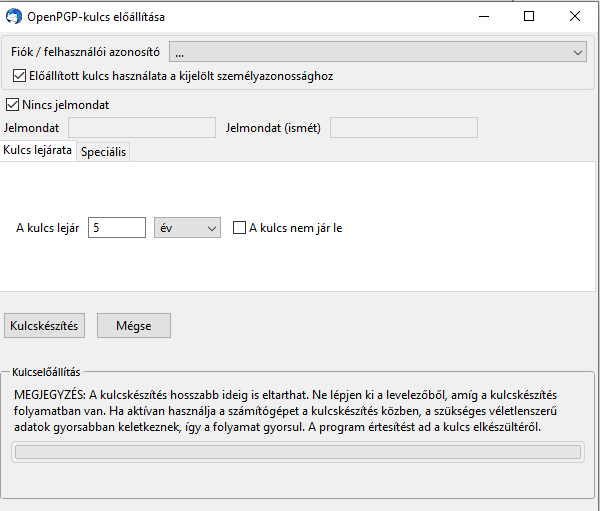
Az Enigmail/p≡p menüpont Kulcskezelő almenüpontjára ha ráklikkelünk akkor létrehozhatunk egy kulcspárt az OpenPGP-kulcs előállítóval, s ahogy látható itt bepipálható a „Nincs jelmondat” rész és ugyanúgy lejárati idő nélkül is tudunk generálni egy kulcspárt ha a jelölőnégyzetet bepipáljuk.
Elképzelhető, hogy amikor Thunderbird email klienst feltelepítjük akkor nem fogjuk megtalálni ezt a már sokat hivatkozott Enigmail/p≡p menüpontot. Ebben az esetben telepíteni kell az Enigmail kiegészítőt a Thunderbird alkalmazáson belül az Eszközök / kiegészítők résznél.
Jelmondat nélkül a kezdőknek kényelmesebb
Ez a pEp metodika a kezdők számára szerintem sokkal előnyösebb, mert nem kell vacakolniuk a jelmondattal, illetve annak megjegyzésével, s nem is kell állandóan begépelniük amikor titkos levelet akarnak küldeni vagy fogadni.
Ennek a kényelemnek ugyanakkor az az ára, hogy ellentétben a Kleopátra kulcspár előállítójával, itt nem tudjuk testre szabni a kódolási eljárást (nem válogathatunk).
A létrehozott kulcspár (.asc fájl) importálása
a Thunderbird Email kliensbe!
Mindenekelőtt a legfontosabb, hogy kényelmesen mindenki dolgozni tudjon ezzel az email kliens programmal az, hogy varázsolja elő a menüt. A program ugyanis alapértelmezetten nem mutatja a menüt, ezért a kliens program tetejére kell vinni az egérkurzort és ott jobb klikk, majd pipáljuk ki a „Menüsor” jelölőnégyzetét!
Gmail cím kezelése a Thunderbird email klienssel
Itt a tanácsom, tehát azoknak szól, akik a Thunderbird email kliensükkel a Gmail email címüket szeretnék kezelni. A Thunderbird email kliens a „Postafiók hozzáadása” résznél amikor megadjuk Gmail email címünket és a belépési jelszót, automatikusan felfogja ismerni, hogy a Gmail a bejövő leveleket (IMAP és melyik porton) a kimenő leveleket (SMTP és melyik porton) stb. kezeli.
⚠️ Amit nagyon sokan elfelejtenek az az, hogy a Google fiókban engedélyeztetni kell a Thunderbird email klienst!
Igazából ezek után túlságosan sok tenni valónk már nincs.
„Enigmail/p≡p”menüpont
Ezen belül a „Kulcskezelő” almenüpontra kell kattintani.
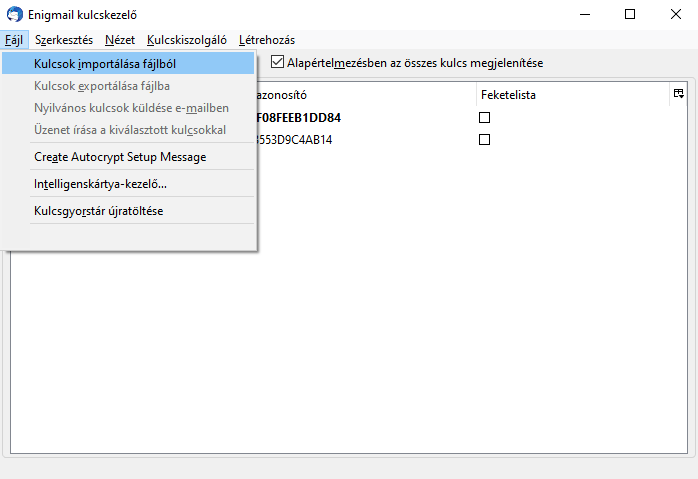
Fájl menü
Itt a „Kulcsok importálása fájlból” almenüpont a számunkra lényeges. Segítségével importáljuk be azt az .asc fájlunkat, amelyet a Kleopátra segítségével hoztunk létre a fentiekben felvázolt 5 lépésben. Az Enigma kulcskezelő tudni fogja, hogy ez fontos fájl és a sajátunk, ezért mások nyilvános kulcsaihoz képest ezt félkövér betűkkel jelzi.
Ha ezzel megvagyunk akkor a Kulcskezelőn belül kattintsunk jobb egérgombbal a beimportált .asc fájlunkra és a következő képen is jól látható menüsort fogjuk kapni, ahol elég sok lehetőségünk akad.
Kulcsok exportálása, importálása
Többek között akad olyan lehetőség is, hogy „Kulcsok exportálása fájlba”.
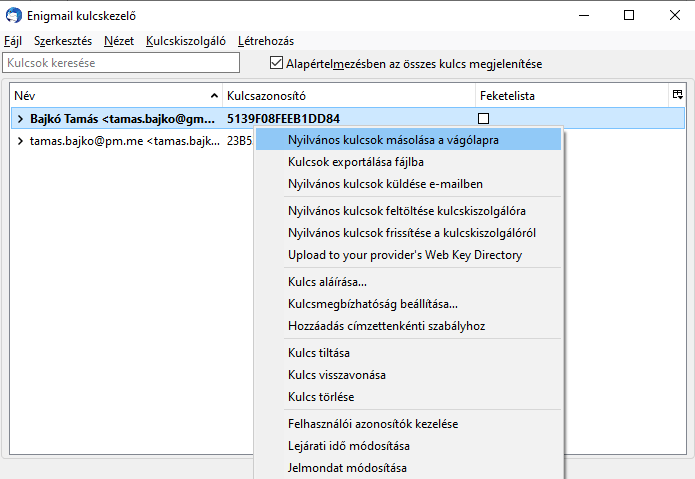
Ez egy lényeges rész, mert itt tudjuk exportálni kizárólag a nyilvános kulcsunkat (public key),
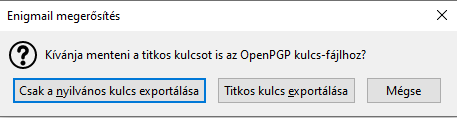
de azért lehetőség akad exportálni a privát kulcsunkat is (private key). Viszont értelemszerű, hogy a privát kulcs exportálásához meg kell adnunk azt a jelmondatot, amit akkor adtunk meg, amikor a Kleopátra segítségével a kulcspárt létrehoztuk, s amire céloztam, hogy írjuk fel egy cetlire és tegyük a széfbe.
Az Enigmail/p≡p / Kulcskezelő / Kulcsok importálása fájlból rész,
✅ a jövőben is nagyon hasznos lesz számunkra, mert kapcsolataink nyilvános kulcsait itt fogjuk tudni importálni, s ahhoz, hogy kódoltan tudjunk is velük levelet váltani ide kell mindenképpen beimportálni.
Miképpen megy ez a fajta levelezés a gyakorlatban?
A fentiek alapján szerintem jól meglehetett érteni, hogy ez egy
végponttól végpontig (tehát feladótól, a címzettig) történő kódolási / dekódolási eljárás, amely azt igényli, hogy mindkét fél rendelkezzen a másik nyilvános kulcsával.
Ez a gyakorlatban úgy működik, hogy akivel titkosított levelezést szeretnél folytatni, annak küldesz egy email-t, amelynek mellékletében szerepel a saját nyilvános kulcsod. Amikor a címzett a leveled megkapja, elmenti a nyilvántartásába, s amikor válaszol Neked, Ő is megküldi részedre a nyilvános kulcsát. Ezek után már tudtok egymásnak titkosított levelet küldeni.
Egészen pontosan mi is a titkosított levelezés lényege?!
Összefoglalva a titkosított levelezésnek az a lényege, hogy nem csak az email szerveren van titkosított formában jelen az adat (mint például Google Gmail esetében a sima TLS titkosítás),
hanem akkor is titkosítva vannak az adatok amikor az email az egyik email szolgáltatótól (feladó) a másik email szolgáltatóig (címzett) megteszi a maga kis kibertérben lévő vándorútját.
S ez az igazi lényege, hogyha egy hacker rá is akaszkodik a kommunikációs portodra és megpróbálja leszipkázni az általad kiküldött levelet, az égvilágon nem fog semmire menni vele, mert csupán egy kódolt információt fog látni.
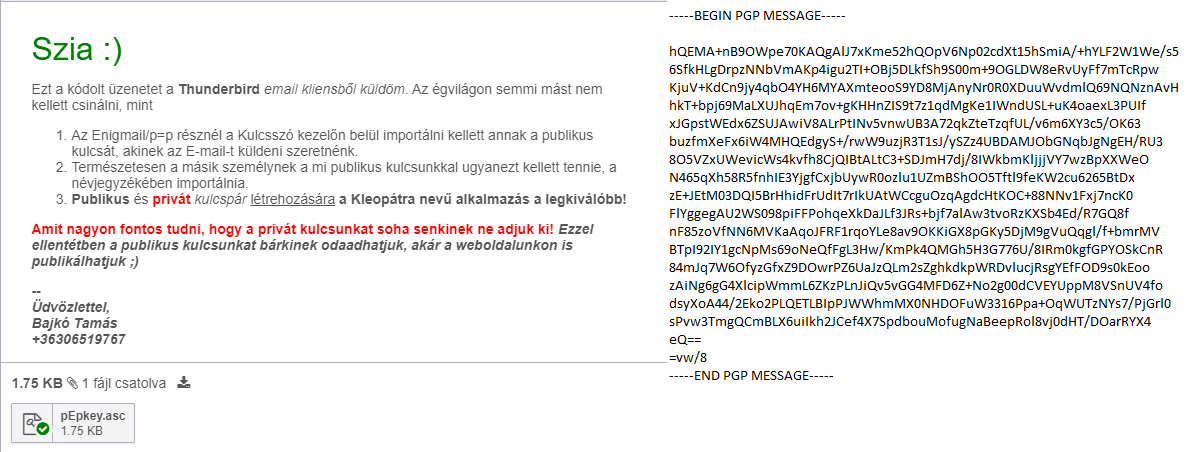
A fenti képpel igyekszem szemléltetni, hogy baloldalt küldtem egy titkosított levelet, amit a címzett dekódolt, ezért tudta elolvasni úgy, ahogyan a baloldalt látszik. Ugyanakkor ha nem rendelkezett volna a nyilvános kulcsommal, akkor csupán a fenti kép jobboldalának megfelelő kódhalmazt látta volna.
👏 Megjegyzem, hogy a kép jobb oldalát annak alapján készítettem, ahogy a Gmail értelmezni tudta 😄 Mivel a Google Mail ügye nem ismerte a beiktatott kódolási eljárást, így számára is titokban marad 😎 🙏 Remélem sikerült emészthetővé tennem a témát.